allrest.blogg.se

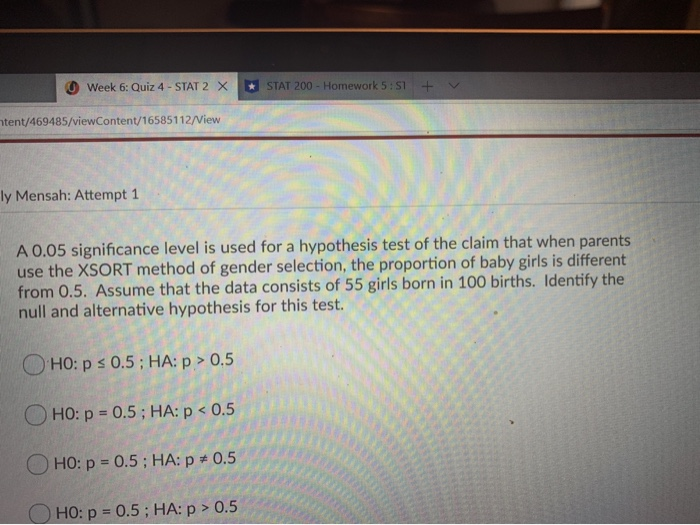
Working assumption: The proportion of girls is p = 0.5 (with no effect from XSORT).Claim: for couples using XSORT, the proportion of girls is p > 0.5.State the conclusion of a hypothesis test in simple, non-technical terms.Ĩ.2 Basics of Hypothesis Testing – Part I Need to understand this example (show concept and process) e.g.2 Chapter problem (continue).Given a value of the test statistic, identify the P-value.Given a significance level, identify the Critical value(s).Given a claim and sample data, calculate the value of the test statistics.Given a claim, identify the null hypothesis and alternative hypothesis, express them in symbolic form.(97 out of 100 is 3 significant)Ĩ.2 Basics of Hypothesis Testing Key Concept Ĩ.2 Basics of Hypothesis Testing – Part I Objective for Part I The other is that the assumption is not true, i.e. One explanation is that extremely rare event happened. There is no sufficient evidence that Gender Choice is effective (common sense) (52 out of 100 is not significant) b.

What should we conclude about the assumption? Sol. b.Ĭonsisting of 52 girls Consisting of 97 girls A product named “Gender Choice” - The Ad claims “increase your chances of having a girl up to 80%” - Assumption: Gender Choice had no effect - If 100 couples using Gender Choice have 100 babies a. Rare Event Rule for Inferential Statistics: If, under a given assumption, the probability of a particular observed event is extremely small, we conclude that the assumption is probably not correct. Examples: Genetics, Business, Medicine, Aircraft Safety, Quality Control. A hypothesis test (or test of significance) is a standard procedure for testing a claim about a property of a population.